 Vous parcourez peut-être ces lignes parce que vous venez de lire le billet publié dans Le Monde, à la une du cahier « Science & Techno » du samedi 9 juin 2012, et que vous avez voulu en savoir un peu plus ? Alors bienvenue !
Vous parcourez peut-être ces lignes parce que vous venez de lire le billet publié dans Le Monde, à la une du cahier « Science & Techno » du samedi 9 juin 2012, et que vous avez voulu en savoir un peu plus ? Alors bienvenue !
Le format de cette « carte blanche » oblige à la concision, et ne permet guère ni de créditer ni a fortiori de citer de façon suffisamment détaillée les recherches et les publications sur lesquelles je me suis appuyé pour la rédiger. Aussi, tant que durera cette tribune (et je viens d’apprendre qu’elle continuera de m’être offerte toute l’année prochaine), je vous propose de retrouver ici, au moment de la parution de chacune de ces « cartes blanches », un billet plus long dans lequel j’essaierai de développer mon propos, et d’apporter quelques suggestions de lectures : ce sera une façon de rendre à mes collègues ce que je leur aurai emprunté pour écrire ces courts billets.
Les Français inégaux face aux vacances
Pour cette dernière carte blanche avant l’interruption estivale, j’avais dans un premier temps imaginé prendre pour objet les vacances, et en particulier la persistance, relativement méconnue, des inégalités de départs en vacances. J’aurais ainsi commencé par rappeler que quand on veut mesurer quelque chose, il faut d’abord le définir, et qu’il faut donc préalablement s’entendre sur une définition de ce que c’est que « partir en vacances ». Si on retient la définition de l’INSEE, qui l’emprunte à l’Organisation mondiale du tourisme, sont comptés comme « départs en vacances » les déplacements d’au moins quatre nuits consécutives hors du domicile, à l’exclusion des déplacements professionnels, des voyages d’études, des séjours motivés par la maladie ou le décès d’un proche et des séjours de santé dans des établissements spécialisés.
Munis de cette définition, qu’observe-t-on ? Il y a une dizaine d’années, un article de Céline Rouquette dans Economie et statistique rappelait la persistance des inégalités de départs en vacances au cours des années 1990. Dix ans plus tard, le taux de départ a régressé dans l’ensemble de la population, puisque aujourd’hui c’est à peine la moitié (53%) des Français qui partent en vacances au moins une fois dans l’année, contre les deux tiers au cours des années 1990. Et surtout, les disparités sont toujours là : 71% des cadres partent en vacances au moins une fois dans l’année, contre seulement 41% des ouvriers, selon une étude du CREDOC.
Comment mesurer les inégalités ?
Juste avant l’été, je voulais prendre ce « prétexte » et cet exemple pour expliquer que les enquêtes sociologiques, contrairement aux expériences des sciences comme la biologie ou la physique, ne produisent que rarement des « découvertes », et que leurs résultats s’énoncent rarement sous la forme de « lois » immuables. Peu de découvertes donc, mais souvent, d’indispensables rappels : contre les discours enchantés de toutes sortes, il s’agissait de montrer que le travail sociologique a donc d’abord pour vocation de mesurer, décrire et tenter de démonter les mécanismes de production et de reproduction des inégalités qui persistent en France dans de nombreux domaines de la vie sociale, en matière de départs en vacances comme on vient de le voir, mais aussi bien sûr en matière d’éducation, de travail, de salaires, de santé, d’accès aux loisirs, de sentiment d’insécurité… Sans ce travail parfois fastidieux et un peu désespérant, mais absolument fondamental, que d’ailleurs l’Observatoire des inégalités s’efforce de rendre le plus visible possible, est-ce que nous n’aurions pas tendance à oublier que les salaires des femmes restent 20% plus faibles que ceux des hommes, que l’espérance de vie des cadres dépasse toujours de six ans celle des ouvriers, et donc que 75 ans après l’instauration des congés payés, encore moins de la moitié d’entre eux partent en vacances ?
Mais arrivé à ce point, je me suis dit que la question sans doute la plus intéressante à traiter dans cette carte blanche, c’était de savoir comment ces inégalités ont évolué au cours des dernières décennies, et si la société française est devenue moins inégalitaire ou si elles sont creusées au contraire. La question est facile à formuler, la réponse l’est beaucoup moins. Comment, en effet, mesure-t-on les inégalités ? Pour rester dans l’actualité, à quelques jours des épreuves du baccalauréat, j’ai voulu prendre un exemple simple, que vous pouvez facilement représenter sur une feuille de papier dans un tableau à deux lignes et deux colonnes : celui de l’évolution des inégalités d’obtention du précieux sésame. Il y a un demi-siècle, 45% des enfants de cadres l’obtenaient, contre seulement 5% des enfants d’ouvriers ; aujourd’hui, 90% des enfants de cadres sont bacheliers, contre 45% des enfants d’ouvriers. Voici ce tableau très simple, que je ne pouvais malheureusement pas reproduire dans la carte blanche, mais qui aide pourtant bien à visualiser les inégalités et leurs évolutions :
Les inégalités ont-elles augmenté ou diminué ? Si on mesure les différences entre ces proportions, elles semblent avoir augmenté (l’écart passe de 45-5=+40 points à 90-45=+45 points). Mais si on mesure les inégalités par un « rapport », elles semblent au contraire avoir diminué : en 1960, la proportion des enfants de cadres qui devenaient bacheliers était 9 fois plus grande (45/5) que celle des enfants d’ouvriers, elle est désormais seulement 2 fois plus grande (90/45)…
Non seulement ces deux façons de mesurer les inégalités se contredisent, mais en plus elles ne sont pas forcément adaptées à la comparaison de pourcentages, parce que ceux-ci… ne peuvent pas dépasser 100% : pour maintenir un taux d’obtention du bac 9 fois plus élevé que celui des enfants d’ouvriers, les enfants de cadres devraient désormais… être 405% à l’obtenir !
Il faut donc recourir à des indices qui tiennent compte du fait que sur le chemin qui mène ne serait-ce qu’aux fameux « 80% d’une classe d’âge au baccalauréat » (c’était l’objectif à l’horizon 2000, qui avait été fixé en 1985 par Jean-Pierre Chevènement, le ministre de l’éducation de l’époque), les dernières longueurs sont plus difficiles à parcourir que les premières. Pour en tenir compte, il y a au moins deux indicateurs concurrents envisageables. Le premier consiste à diviser la progression effectuée par le maximum de la progression possible : entre 1960 et aujourd’hui, les enfants de cadres ont parcouru (90-45)/(100-45) = 82% du chemin qui les séparaient de la réussite totale au baccalauréat, et les enfants d’ouvriers seulement (45-5)/(100-5) = 42%% de ce chemin. Tenons-nous enfin notre réponse ? Les inégalités scolaires ont-elles augmenté ?
Le problème, c’est que le second indicateur possible, celui qui en réalité s’est imposé parmi les sociologues, dit plutôt le contraire. Il consiste à calculer et comparer plutôt des odds ratio, ou « rapports des chances relatives », autrement dit les rapports entre le taux de réussite et le taux d’échec. Par exemple, aujourd’hui, un enfant de cadres a 90/(100-90) = 9 fois plus de chances d’obtenir le bac que de ne pas l’obtenir. Et à l’aune de ces rapports de chances relatives, les inégalités scolaires auraient plutôt diminué : en 1960, les enfants de cadres avaient [45/(100-45)]/[5/(100-5)] = 15,5 fois plus de chances que les enfants d’ouvriers d’obtenir le bac plutôt que de ne pas l’obtenir ; aujourd’hui, ils ont « seulement » [90/(100-90)]/[45/(100-45)] = 11 fois plus de chances.
« Conclusions roses » et « conclusions noires »
Si les phrases qu’il faut faire pour énoncer ces odds ratio sont parfois un peu alambiquées, avec ces « plutôt que le contraire » qui les parsèment, il faut bien reconnaître qu’ils sont très séduisants, parce qu’ils sont faciles à calculer (pas besoin de logiciel compliqué, une minuscule calculatrice suffit), et qu’ils semblent résoudre de façon très satisfaisante pour l’esprit le problème de la non-linéarité des progressions en pourcentage. Pourtant, pour certains, si les odds ratio se sont imposés depuis les années 1990, en particulier parmi les sociologues de l’éducation, qui en font une grande consommation, ce ne serait pas parce qu’ils mesureraient plus correctement les variations des inégalités, mais parce qu’ils les mesureraient… de façon plus optimiste !
C’est tout le sens de la « controverse » sur la mesure des inégalités, qui traverse la sociologie française depuis le milieu des années 1980. Je n’en donnerai qu’un aperçu rapide, mais voici déjà la bibliographie, dans l’ordre chronologique de parution, des principaux articles qui jalonnent cette passionnante discussion méthodologique :
Combessie Jean-Claude, 1984, « L’évolution comparée des inégalités : problèmes statistiques », Revue française de sociologie, 25(2), 1984, p. 233-254. En ligne : http://www.persee.fr/web/revues/home/prescript/article/rfsoc_0035-2969_1984_num_25_2_3793
Florens Jean-Pierre, 1984, « Inégalité et dépendance statistique », Revue française de sociologie, 25(2), p. 255-263. En ligne : http://www.persee.fr/web/revues/home/prescript/article/rfsoc_0035-2969_1984_num_25_2_3794
Grémy Jean-Paul, 1984, « Sur les différences entre pourcentages et leur interprétation », Revue française de sociologie, 25(3), p. 396-420. En ligne : http://www.persee.fr/web/revues/home/prescript/article/rfsoc_0035-2969_1984_num_25_3_3824
Prévot Jean, 1985, « À propos d’indices et de comparaisons de proportions », Revue française de sociologie, 26(4), p. 601-628. En ligne : http://www.persee.fr/web/revues/home/prescript/article/rfsoc_0035-2969_1985_num_26_4_3987
Combessie Jean-Claude, 2004, « Trente ans de comparaison des inégalités des chances : quand la méthode retenue conditionne la conclusion », Courrier des statistiques, 112, , p. 37-54. En ligne : http://www.insee.fr/fr/ffc/docs_ffc/cs112e.pdf
Vallet Louis-André, 2007, « Sur l’origine, les bonnes raisons de l’usage, et la fécondité de l’odds ratio », Courrier des statistiques, 121-122, p. 59-65. En ligne : http://www.insee.fr/fr/ffc/docs_ffc/cs121k.pdf
Combessie Jean-Claude, 2007, « Réponse à Louis-André Vallet », Courrier des statistiques, 121-122, p. 66. En ligne : http://www.insee.fr/fr/ffc/docs_ffc/cs121l.pdf
Combessie Jean-Claude, 2011, « Analyse critique d’une histoire des traitements statistiques des inégalités de destin. Le cas de l’évolution des chances d’accès à l’enseignement supérieur, Actes de la recherche en sciences sociales, n° 188, p. 4-31.
Comme on peut le voir à travers cette bibliographie, c’est une affaire qui tenait particulièrement à cœur à Jean-Claude Combessie. Il m’est difficile de résumer son argument en quelques lignes, mais la lecture de son dernier article, paru en 2011 dans les Actes de la recherche en sciences sociales, la revue créée en 1975 par Pierre Bourdieu, peut en offrir une très bonne synthèse. Malheureusement, l’article n’étant disponible en ligne qu’en accès restreint sur Cairn, vous pouvez aussi lire son article de 2004, et celui publié par Louis-André Vallet en 2007, dans le Courrier des statistiques, tous les deux d’accès facile et surtout gratuit. Voici de quoi il retourne : Jean-Claude Combessie passe en revue les différentes façons différentes de mesurer les inégalités que nous avons évoquées précédemment (différence, rapport, taux de variation par rapport au maximum de variation, odds ratio), et les soumet à l’épreuve de la mesure des évolutions de différentes formes d’inégalités scolaires depuis trois décennies, pour démontrer que le recours à l’odds ratio aboutit plus souvent que les autres mesures, et en particulier plus souvent que le taux de variation par rapport au maximum de variation, à des « conclusions roses », autrement dit à des mesures suggérant une diminution des inégalités.
L’odds ratio, une « révolution conservatrice » ?
Toute la question est ensuite de savoir s’il y a un indicateur qui est meilleur que les autres. Pour Louis-André Vallet c’est le cas : il s’agit de l’odds ratio, qu’il y a de « bonnes raisons statistiques » de considérer comme l’indicateur le plus « naturel » pour rendre compte des évolutions plafonnées, comme c’est le cas pour les pourcentages. Pour Jean-Claude Combessie, il n’y au contraire rien de naturel là-dedans, et il faut plutôt s’interroger sur les raisons qu’ont les sociologues de privilégier cet indicateur, qu’il soupçonne de ne pas être toujours « statistiques ». En effet, dans le second volet de sa démonstration, Jean-Claude Combessie reprend les données analysées dans la littérature des trente dernières années sur les inégalités scolaires (les principaux articles sont signalés dans la bibliographie à la fin de ce billet), calcule les différents indicateurs pour voir s’ils aboutissent à des conclusions « noires » ou « roses », et compare avec ceux effectivement utilisés par les auteurs des articles : il apparaît alors que plus souvent qu’attendu, ceux-ci tendent à utiliser les indicateurs qui permettent de conclure à une diminution des inégalités scolaires. Dans certains cas, les mêmes auteurs peuvent changer d’indicateur d’un article à l’autre, pour choisir justement tel ou tel en fonction des conclusions « optimistes » auquel il permet de parvenir.
Pour Jean-Claude Combessie, aucun indicateur n’étant ni « statistiquement » ni « sociologiquement » meilleur qu’un autre, il faut donc s’interroger sur les significations sociales et politiques des choix effectués par les sociologues de l’éducation, interrogation qui le conduit à décrire le succès de l’odds ratio comme un symptôme d’une « révolution conservatrice » dans la mesure des inégalités, qui tend à décrire des améliorations là où l’orthodoxie statistique précédente tendait à décrire des aggravations.
Pour un éclectisme statistique
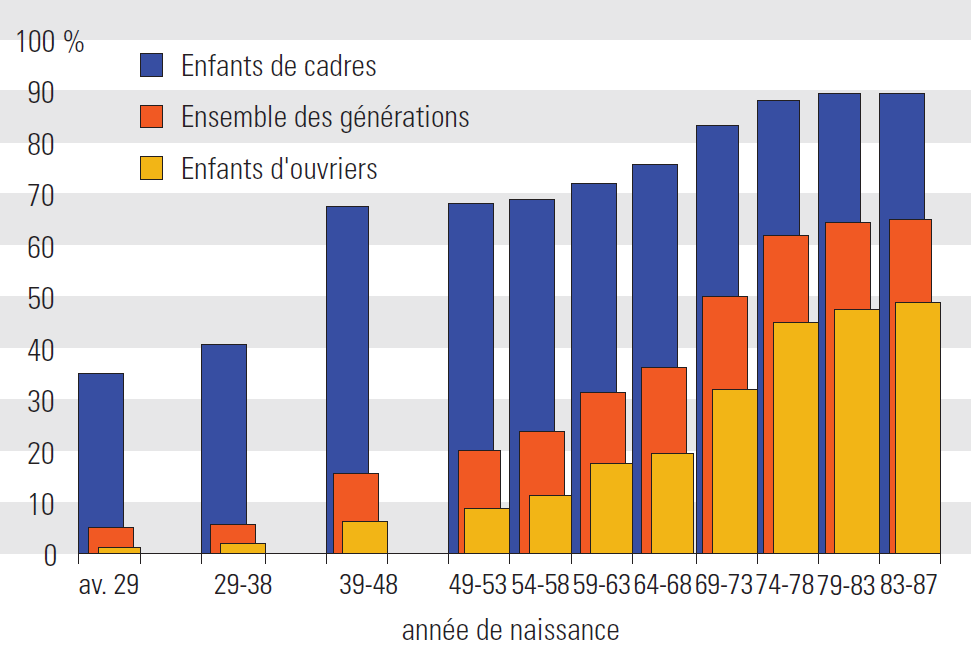
Quelle conclusion pratique faut-il en tirer ? Pour y voir plus clair pratiquement, on peut reprendre l’exemple de l’évolution des inégalités d’obtention du baccalauréat, cette fois en examinant une série plus complète de données. Celle-ci n’est pas très facile à trouver, mais on peut se servir du graphique ci-dessous, publié dans la dernière édition de L’état de l’école, une publication du Ministère de l’éducation nationale, pour tenter de la reconstituer :
Dans le tableau ci-dessous, j’ai dans les colonnes de gauche essayé de reconstituer approximativement les taux d’obtention du baccalauréat dans les générations successives d’enfants de cadres et d’enfants d’ouvriers, puis dans les colonnes de droite j’ai mesuré les variations de ces taux avec les quatre indicateurs évoqués depuis le début de ce billet :
Qu’y voit-on ? Que dans l’ensemble, il n’arrive presque jamais aux rapports et aux odds ratio de rendre des « conclusions noires », alors que c’est très clairement le cas en particulier du rapport entre l’écart et l’écart maximum possible. Que faut-il faire dans ces cas-là ? Une position relativement simple consiste à favoriser l’éclectisme statistique, et donc à présenter les résultats divergents rapportés par les différents indicateurs. On indiquera ainsi par exemple qu’entre les enfants de cadres et les enfants d’ouvriers nés entre 1979 et 1983, et qui ont donc atteint l’âge normal du baccalauréat entre 1997 et 2001, les inégalités d’obtention du bac avaient diminué si l’on considère l’odds ratio, mais augmenté si l’on considère le rapport entre l’écart observé et l’écart maximum possible, sans qu’il soit possible de décider qu’un de ces deux indicateurs est « meilleur » que l’autre. D’un côté, on peut dire par exemple que l’odds ratio permet de rendre compte de façon satisfaisante de la réduction de l’écart entre des valeurs dont les variations sont plafonnées, comme c’est le cas pour les pourcentages ; mais de l’autre côté, le taux de variation par rapport au maximum de variation possible rend bien compte des perceptions subjectives des inégalités restantes que peuvent avoir les individus : à mesure que leurs situations s’améliorent, par exemple en matière scolaire, les générations successives deviennent plus sensibles à des écarts plus petits, qui auraient auparavant été tenus pour négligeables.
L’évolution des inégalités scolaires, une équation complexe
Jusqu’ici, j’ai essayé de faire attention à ne parler que des inégalités d’obtention du baccalauréat entre enfants de cadres et enfants d’ouvriers. En réalité, si l’on souhaite juger de l’évolution des « inégalités scolaires en général », alors l’équation devient encore un peu plus complexe, et ce n’est plus seulement une question de choix d’indicateurs. D’une part en effet, pour reprendre le titre d’un article publiée par Françoise Oeuvrard il y a plus de trente ans, il ne faut pas confondre « démocratisation » et « élimination différée » : l’éventuelle réduction des inégalités d’obtention du bac s’est accompagnée d’une diminution du pouvoir discriminant de celui-ci sur le marché du travail, au profit de niveaux supérieurs d’études où l’on n’assiste pas à la même réduction des inégalités. Comment mesurer les effets de ce déplacement sur l’évolution générale des inégalités ? Il y a quelques hypothèses intéressantes à ce sujet dans l’article de Claude Thélot et Louis-André Vallet sur « la réduction des inégalités sociales devant l’école depuis le début du siècle » (2000).
Et d’autre part, il y a au moins un autre phénomène à prendre compte si on veut mesurer l’évolution générale des inégalités scolaires : il ne suffit pas de mesurer les inégalités entre enfants de cadres et d’ouvriers, ou plus généralement entre enfants de différents milieux sociaux, il faut aussi tenir compte du fait que la structure sociale elle-même se modifie, que la distribution des élèves entre les différents milieux sociaux change, et que par exemple il y a de plus en plus d’enfants de cadres et de moins en moins d’enfants d’ouvriers. Même à taux de réussite scolaire inchangés pour ces deux catégories, ces modification de sa structure suffisent à modifier le niveau global des inégalités dans l’ensemble de la population considérée. Il faut alors d’autres indicateurs, comme par exemple le coefficient de Gini, mais c’est une autre histoire… Ce sera pour un prochain billet !
Références bibliographiques
Barbut Marc, 2007, La Mesure des inégalités. Ambiguïtés et paradoxes, Genève, Droz
Duru-Bellat Marie, Kieffer Annick, 2000, « La démocratisation de l’enseignement en France. Polémiques autour d’une question d’actualité », Population, 55(1), p. 51-80. En ligne : http://www.persee.fr/web/revues/home/prescript/article/pop_0032-4663_2000_num_55_1_7097
Euriat Michel, Thélot Claude, 1995, « Le recrutement social de l’élite scolaire en France. Évolution des inégalités de 1950 à 1990 », Revue française de sociologie, 36(3), p. 403-438. En ligne : http://www.persee.fr/web/revues/home/prescript/article/rfsoc_0035-2969_1995_num_36_3_5065
Florens Jean-Pierre, 1984, « Inégalité et dépendance statistique », Revue française de sociologie, 25(2), p. 255-263. En ligne : http://www.persee.fr/web/revues/home/prescript/article/rfsoc_0035-2969_1984_num_25_2_3794
Goux Dominique, Maurin Éric Maurin, 1997, « Démocratisation de l’école et persistance des inégalités », Économie et Statistique, 306, p. 27-39. En ligne : http://www.persee.fr/web/revues/home/prescript/article/estat_0336-1454_1997_num_306_1_2570
Grémy Jean-Paul, 1984, « Sur les différences entre pourcentages et leur interprétation », Revue française de sociologie, 25(3), p. 396-420. En ligne : http://www.persee.fr/web/revues/home/prescript/article/rfsoc_0035-2969_1984_num_25_3_3824
Hoibian Sandra, 2010, « Vacances 2010 : Les contraintes financières favorisent de nouveaux arbitrages », Crédoc, enquête « Conditions de vie et Aspirations des Français ». En ligne : http://www.credoc.fr/pdf/Sou/vacances_ete_2010.pdf
Maurin Louis, 2008, «L’Observatoire des inégalités : un état des lieux », Informations sociales, n° 148, p. 106-107. En ligne : http://www.cairn.info/revue-informations-sociales-2008-4-page-106.htm
Maurin Louis, Savidan Patrick (dir.), 2008, L’état des inégalités en France. Données et analyses, Belin
Oeuvrard Françoise, 1979, « “Démocratisation” ou élimination différée ? Note sur l’évolution du recrutement social de l’enseignement secondaire en France, entre 1958 et 1976 », Actes de la recherche en sciences sociales, 30, p. 87-97. En ligne : http://www.persee.fr/web/revues/home/prescript/article/arss_0335-5322_1979_num_30_1_3491
Prévot Jean, 1985, « À propos d’indices et de comparaisons de proportions », Revue française de sociologie, 26(4), p. 601-628. En ligne : http://www.persee.fr/web/revues/home/prescript/article/rfsoc_0035-2969_1985_num_26_4_3987
Prost Antoine 1986, L’enseignement s’est-il démocratisé ?, Paris, PUF
Rouquette Céline, 2001, « Départs en vacances: la persistance des inégalités », Économie et Statistique, 345, 1, p. 33-53. En ligne : http://www.insee.fr/fr/ffc/docs_ffc/ES345B.pdf
Thélot Claude, Vallet Louis-André, 2000, « La réduction des inégalités devant l’école depuis le début du siècle », Economie et Statistique, n° 334, p. 3-32. En ligne : http://www.insee.fr/fr/ffc/docs_ffc/es334a.pdf
Vallet Louis-André, 1988, « L’évolution de l’inégalité des chances devant l’enseignement. Un point de vue de modélisation statistique », Revue française de sociologie, 29(3), p. 395-423. En ligne : http://www.persee.fr/web/revues/home/prescript/article/rfsoc_0035-2969_1988_num_29_3_2524
Vallet Louis-André, 2007, « Sur l’origine, les bonnes raisons de l’usage, et la fécondité de l’odds ratio », Courrier des statistiques, 121-122, p. 59-66. En ligne : http://www.insee.fr/fr/ffc/docs_ffc/cs121k.pdf













{ 9 commentaires… lisez-les ci-dessous ou ajoutez un commentaire }